STEM Teacher Training Network of the Netherlands

nl

STEM Teacher Training Network of the Netherlands

Problem solving

Problem solving is more than just solving a problem.

Definition

Problem solving refers more to the process that leads to solving the problem than to finding the solution itself. In problem solving, the ability to use heuristics and a mathematical attitude are important. In general, a number of phases can be distinguished in problem solving:

  • describe the problem;
  • make a plan to solve the problem;
  • solve the problem;
  • look back on what you did.

Below, we show some graphic representations that summarise (mathematical) problem solving in a few ‘steps’. In all these models, the order of the steps and the coherence of the steps is less fixed than the pictures suggest.

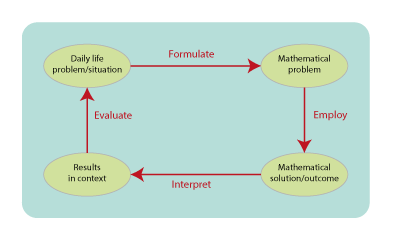
2003 – Pisa

The PISA 2003 Assessment Framework. Paris: OECD.

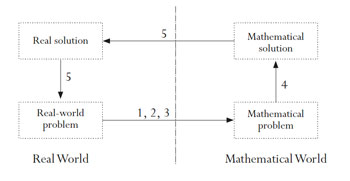
2009 – Blum

Blum, W. and Borromeo Ferri, R. (2009). Mathematical Modelling: Can It Be Taught And Learnt? Journal of Mathematical Modelling and Application

2015 – Pisa modeling cycle

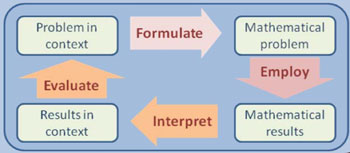
PISA 2015 draft mathematics framework. Paris: OECD.

  • (2003). The PISA 2003 Assessment Framework (PDF). Paris: OECD.
  • (2013). PISA 2015 draft mathematics framework (PDF). Paris: OECD.
  • (2015). Syllabus rekenen 2f en 3f vo en mbo (PDF). Utrecht: College voor Toetsen en Examens.
  • Blomhøj, M. and Jensen, T. H. (2003). Developing mathematical modelling competence: conceptual clarification and educational planning (PDF) Teaching Mathematics and its Applications, 22(3), 123-139. 10.1093/teamat/22.3.123
  • Blum, W. and Niss, M. (1991). Applied Mathematical Problem Solving, Modelling, Applications, and Links to Other Subjects: State, Trends and Issues in Mathematics Instruction (PDF) Educational Studies in Mathematics, 22(1), 37-68
  • Blum, W. and Borromeo Ferri, R. (2009). Mathematical Modelling: Can It Be Taught And Learnt? (PDF) Journal of Mathematical Modelling and Application, 1, 45-58
  • Schoenfeld, A. H. (1992). Learning to think mathematically: problem solving, metacognition, and sense making mathematics (PDF). In D. A. Grouws (Ed.), Handbook of Research on Mathematics Teaching (pp. 334-370). New York: MacMillan.