Probleemoplossen

Probleemoplossen (problem solving in het Engels) is meer dan alleen het oplossen van een probleem.

Definitie

Met probleemoplossen doelt men meer op het proces dat leidt tot het oplossen van het probleem dan op het vinden van de oplossing zelf. Bij probleemoplossen zijn het kunnen hanteren van heuristieken en het hebben van een wiskundige houding van belang. Over het algemeen kunnen bij probleemoplossen een aantal fasen worden onderscheiden:

• beschrijf het probleem;
• maak een plan om het probleem op te lossen;
• los het probleem op;
• blik terug op wat je precies gedaan hebt.

Toelichting bij het plaatje Probleemoplossen

De vier bolletjes Probleem in het dagelijks leven. Het is een ‘echt’ probleem waar je tegenaan loopt, geen ‘denkbeeldig’ probleem, hoewel dat in het onderwijs niet altijd geldt. In het onderwijs mag best een denkbeeldig probleem gesteld worden, maar ook dan helpt het dat je kunt bedenken dat het jouw probleem zou kunnen zijn in een echte situatie. Rekenkundig probleem. Bij dit schema beperken we ons tot problemen waar een of meer reken/wiskundige aspecten een rol spelen. Bij het oplossen van het probleem moet er gerekend worden, wil je tot een oplossing komen. Deze stap leidt er toe dat je weet wat er berekend moet worden. Uitkomst bewerking(en). Na het vaststellen wat het rekenkundig probleem is vindt de feitelijke berekening plaats. Dit kan een eenvoudig optelling zijn of iets dergelijks, maar ook een opeenvolging van rekenkundige handelingen, afhankelijk van de complexiteit van het probleem en de situatie. Oplossing van probleem. Door de voorgaande stappen wordt er een oplossing gevonden.

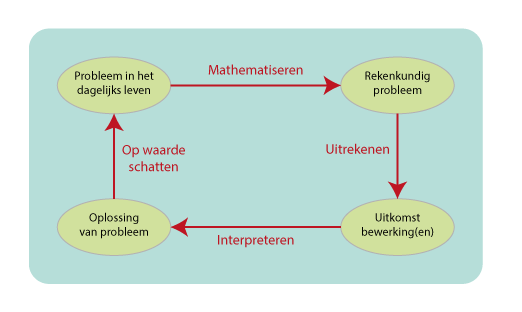
De vier pijltjes Mathematiseren. Bij de stap van het probleem uit het dagelijks leven naar een rekenkundig probleem is er al veel ‘wiskundige’ kennis nodig. We noemen dat ook wel het ‘mathematiseren’ van het probleem. je weet dan bijv. dat je moet gaan schatten, dat je een bepaalde berekening moet gaan uitvoeren, etc. Uitrekenen. Dit is het gebied van de ‘basisvaardigheden rekenen’ inclusief handig gebruik van de rekenmachine, etc. Interpreteren. Door het uitrekenen is er een uitkomst wat betreft het rekenkundig probleem. Dit is bijvoorbeeld een getal op een papiertje, op een rekenmachine of in een spreadsheet. Het getal moet dan weer betekenis krijgen in de context waar het probleem speelt (voorzien van een label, een grootheid, etc.) Op waarde schatten. Dit is een controlestap. Je hebt de stappen doorlopen en je hebt een uitkomst, maar je gaat in feite weer terug naar je oorspronkelijke vraagstelling en je bedenkt of jouw oplossing ‘past’ bij jouw probleem.

Integrale aandacht voor ‘wiskundig denken’

In zekere zin is het nadenken over probleemoplossen (in relatie tot wiskundeonderwijs) ook een poging om naast de aandacht voor de reken-wiskundige handeling ook meer aandacht te krijgen (in en buiten de wiskundeles) voor denkactiviteiten.

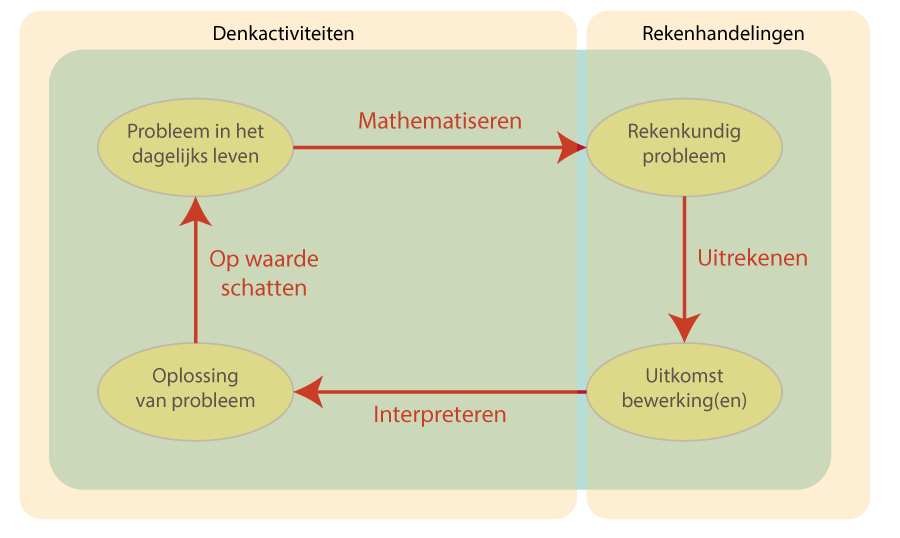
Zie ook het werk van o.a. Paul Drijvers (Drijvers, 2018) op dit vlak.

Geschiedenis van het denken over probleemoplossen (in relatie tot wiskundeonderwijs)

Hieronder laten we enkele grafische representaties zien die het (wiskundig) probleemoplossen samenvatten in enkele ‘stappen’. Bij al deze modellen geldt dat de volgorde van de stappen en de samenhang van de stappen minder vastligt dan de plaatjes suggereren. Het denken over probleemoplossen kent een lange geschiedenis, langer dan we hier nu schetsen. Eerder werk werd al uitgevoerd door o.a. Schoenfeld (1987 en 1992) en Freudenthal (1983).

2002 – Verschaffel, Greer en De Korte

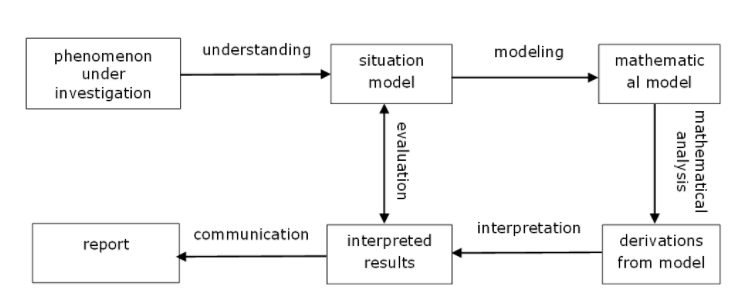
Everyday knowledge and mathematical modeling of school word problems, p. 258 (Verschaffel et al, 2002).

2003 – Pisa

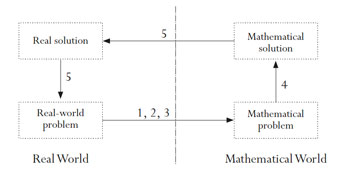
The PISA 2003 Assessment Framework. Paris: OECD.

2009 – Blum

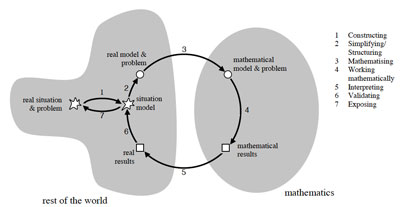
Blum, W. and Borromeo Ferri, R. (2009). Mathematical Modelling: Can It Be Taught And Learnt? Journal of Mathematical Modelling and Application

2015 – Pisa modeling cycle

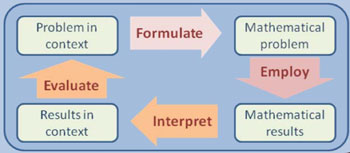
PISA 2015 draft mathematics framework. Paris: OECD.

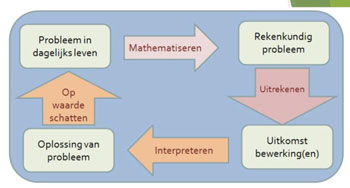
Vertaald door Kees Hoogland

2015 – Syllabus rekenen cvte

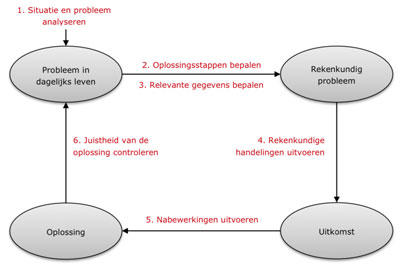
Syllabus rekenen 2f en 3f vo en mbo. Utrecht: College voor Toetsen en Examens.