Reken-wiskundige vaardigheid
| PO | VO | MBO |

|
Denkmodel over hoe de reken-wiskundige vaardigheid is opgebouwd uit verschillende aspecten
Engelse term: Five strands of mathematical proficiency |
Verbeelding van wiskundige vaardigheid
Het is niet eenvoudig om dergelijke samengestelde vaardigheden goed in beeld te brengen. De metafoor van een touw met strengen lijkt een goed beeld te geven.
Engels:
|
Nederlands: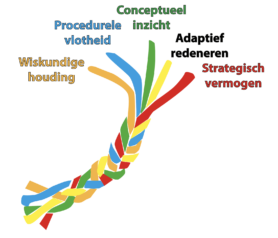
|
Toelichting
In dit model worden vijf onderliggende aspecten onderscheiden.
| Conceptueel inzicht | Conceptual understanding |
| Procedurele vlotheid | Procedural fluency |
| Wiskundige houding | Productive disposition |
| Adaptief redeneren | Adaptive reasoning |
| Strategisch vermogen | Strategic competence |
Conceptueel inzicht
Dit is het begrijpen van wiskundige concepten, operaties en relaties. Zo begrijpt een leerling dat hoe groter de tegel is waarmee hij wil vloeren, hoe minder tegels hij nodig heeft voor een kamer, dan wanneer de oppervlakte van de tegels kleiner is.
Procedurele vlotheid
Het juist, flexibel en efficiënt kunnen toepassen van procedures om (herhaaldelijke) oefeningen van een bepaald type correct te kunnen oplossen. De leerling kan na veel oefenen snel procentrekenen: het getal waarvan we het procent willen berekenen delen door honderd en dit quotiënt vermenigvuldigen met het aantal procent.
Wiskundige houding
Het herkennen van wiskunde als betekenisvol en bruikbaar is van onschatbare waarde. Daarom moet er vaak geoefend worden om wiskundig bekwamer te worden. Succeservaringen zijn hier de sleutel. Een leerling kan voldoening krijgen door zelf in staat te zijn de aflossingstabel van diens lening te begrijpen of het te zien wanneer een leverancier een foute berekening heeft gemaakt ten nadele van diegene die moet betalen.
Adaptief redeneren
Het in staat zijn om kritisch te reflecteren over een antwoord, een oplossingsstrategie te verklaren en de metacognitieve vaardigheid bezitten om zelf gemaakte fouten te kunnen corrigeren. Bij het berekenen van het gemiddelde verkrijgt een leerling een getal dat groter is dan de reeks getallen waarvan hij het gemiddelde moet berekenen. Deze leerling kan dan het antwoord in vraag stellen en nagaan als de juiste procedure werd toegepast, een rekenfout werd gemaakt…
Strategisch vermogen
Het probleem kunnen vertalen naar de juiste wiskundige begrippen, concepten, procedures… Bijvoorbeeld: een leerling tuinbouw moet aarde aanvoeren om een bloembak te vullen. Die leerling zal beseffen dat hij hiervoor het volume van de bloembak moet berekenen en niet de oppervlakte.
Verweven competenties
Deze vijf strengen zijn sterk met elkaar verweven. Wie wiskundig bekwaam is zal deze competenties bezitten maar ook op elkaar laten inwerken. Zo zal een wiskundig bekwaam persoon die een kamervloer wil betegelen niet enkel inzicht hebben in welke wiskundige vorm de kamer die hij wil betegelen heeft (strategisch vermogen en conceptueel inzicht), maar zal die ook weten welke oppervlakteformule hij nodig heeft om het aantal m² tegels hij moet bestellen en correct kunnen uitrekenen (procedurele vlotheid), en zal die bovendien weten dat er verlies is bij het leggen van tegels en dat er geen 5,7 pakken tegels kunnen aangekocht worden (adaptief redeneren), enz.
Bron

|
Een van de bedenkers van dit model: Jeremy Kilpatrick
Bron: Adding it Up, 2001 |
Verwijzingen
- Kilpatrick, J. and Swafford, J. (Eds.). (2002). Helping Children Learn Mathematics (PDF). Washington D.C.: National Academy Press
- Kilpatrick, J., Swafford, J. and Findell, B. (2001). Adding it Up. Helping Children Learn Mathematics. Washington DC, USA: National Academies Press
- Kilpatrick, J. (2001). Understanding mathematical literacy: The contribution of research (PDF) Educational Studies in Mathematics, 47(1), 101-116. doi:10.1023/A:1017973827514
Zie ook Probleemoplossen en Gecijferdheid.


